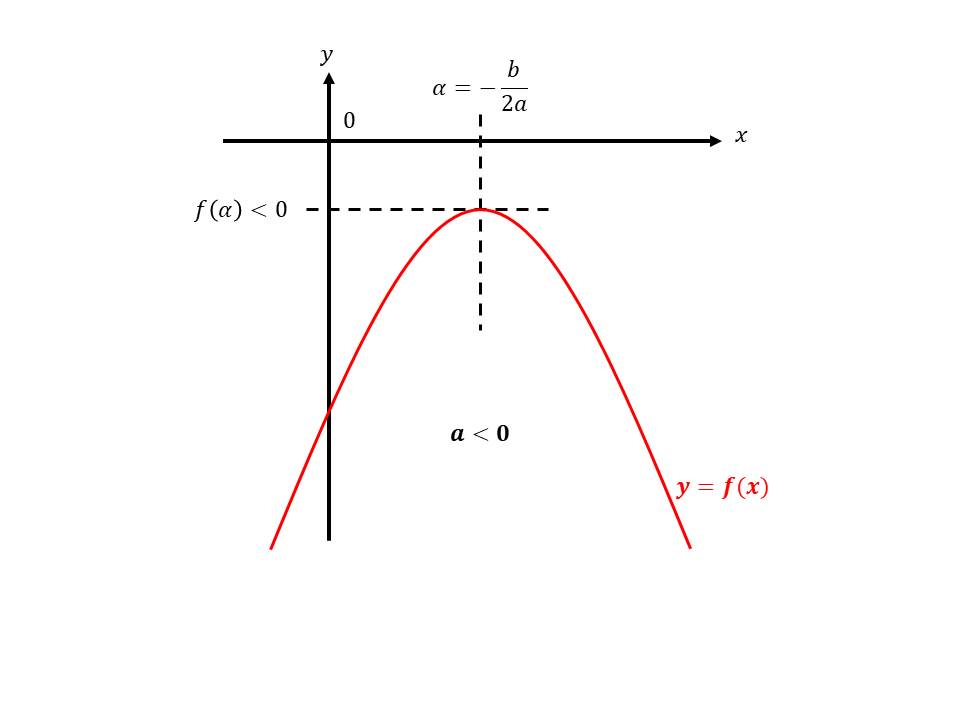
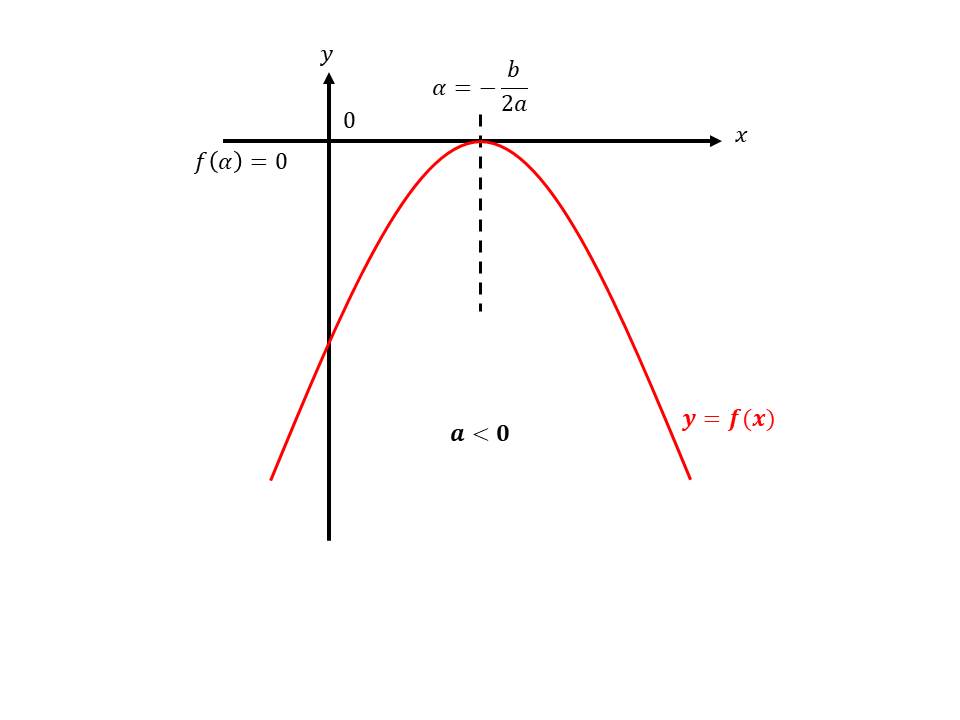
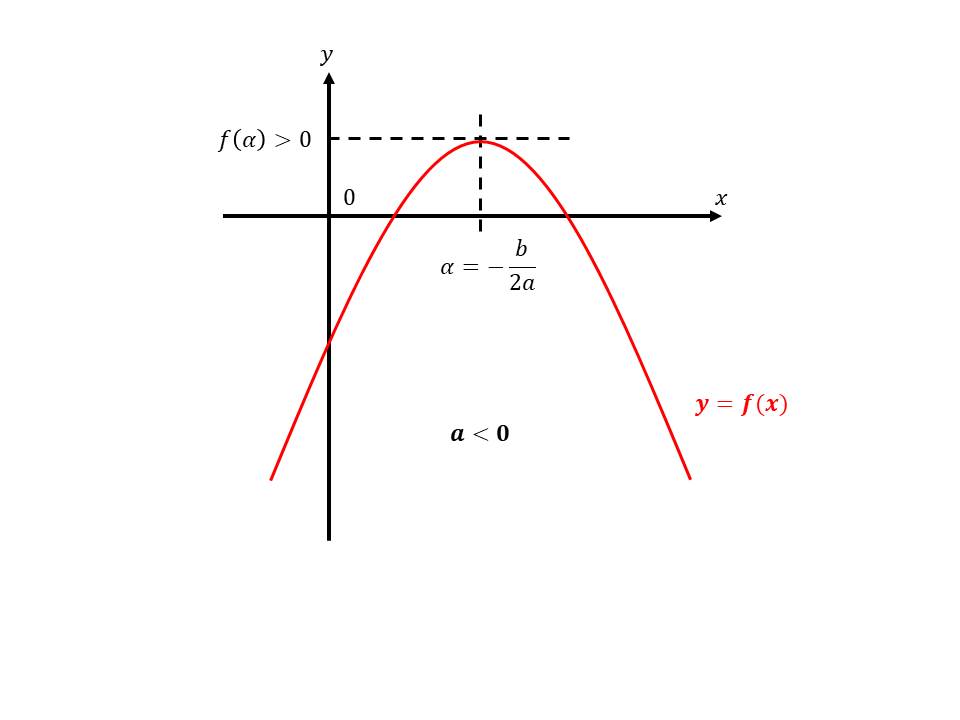
Une fonction du second degré est une fonction de la forme: $$ f(x) = ax^2 + bx + c $$ on supposera que \( a \neq 0 \) sinon la fonction devient une fonction du premier degré: \( f(x) = bx+c \)

Forme canonique:

$$f(x) = a(x-\alpha)^2+\beta$$

Résolution \(f(x) = 0\)

• \(\Delta < 0\)
Pas de solution
Pas de factorisation

• \(\Delta = 0\)
1 seule solution solution - racine double
\(x_0=-\frac{b}{2a}\)
\( f(x) = (x-x_0)^2 \)

• \(\Delta < 0\)
2 solutions distinctes
\(x_1=\frac{-b-\sqrt(\Delta)}{2a}\)
\(x_2=\frac{-b+\sqrt(\Delta)}{2a}\)
\( f(x) = (x-x_1)(x-x_2) \)

Configurations

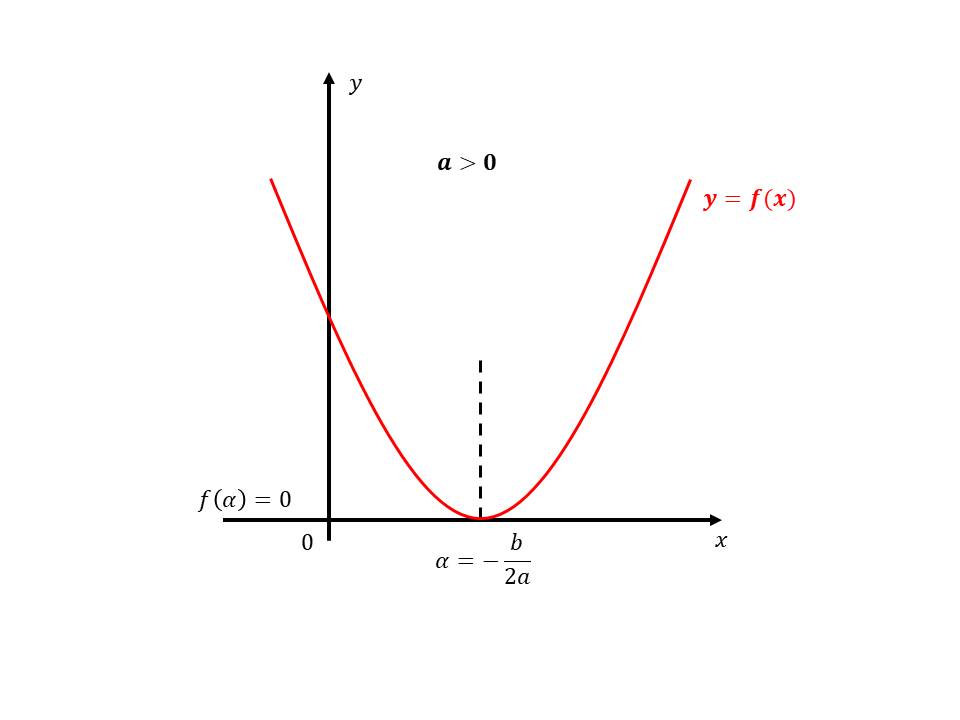
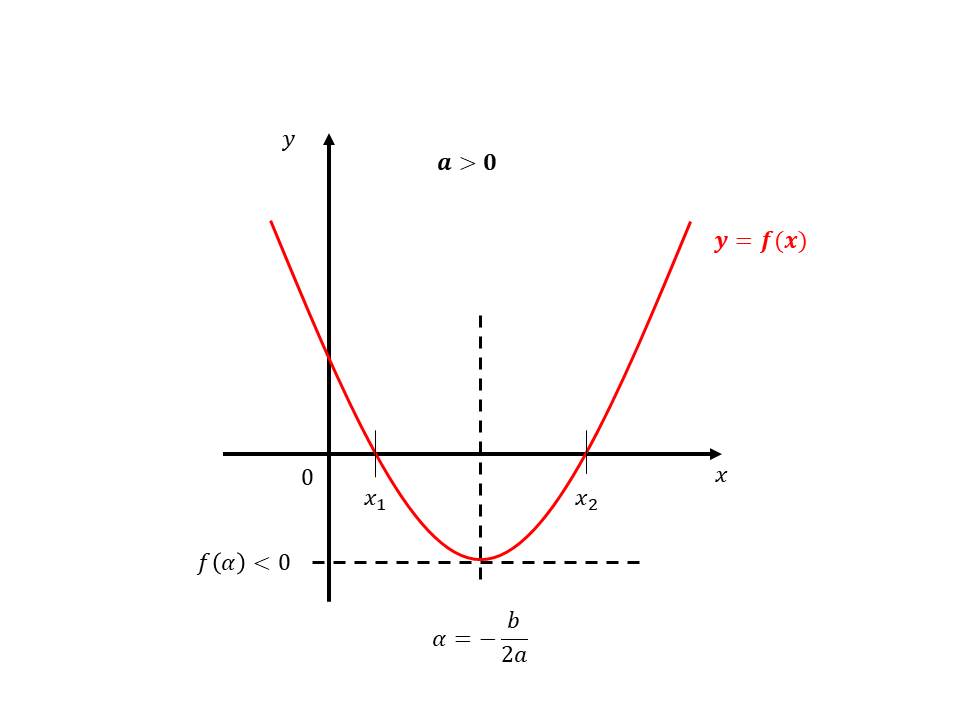
\(a>0\)

• \(\Delta < 0\)


• \(\Delta = 0\)





• \(\Delta > 0\)

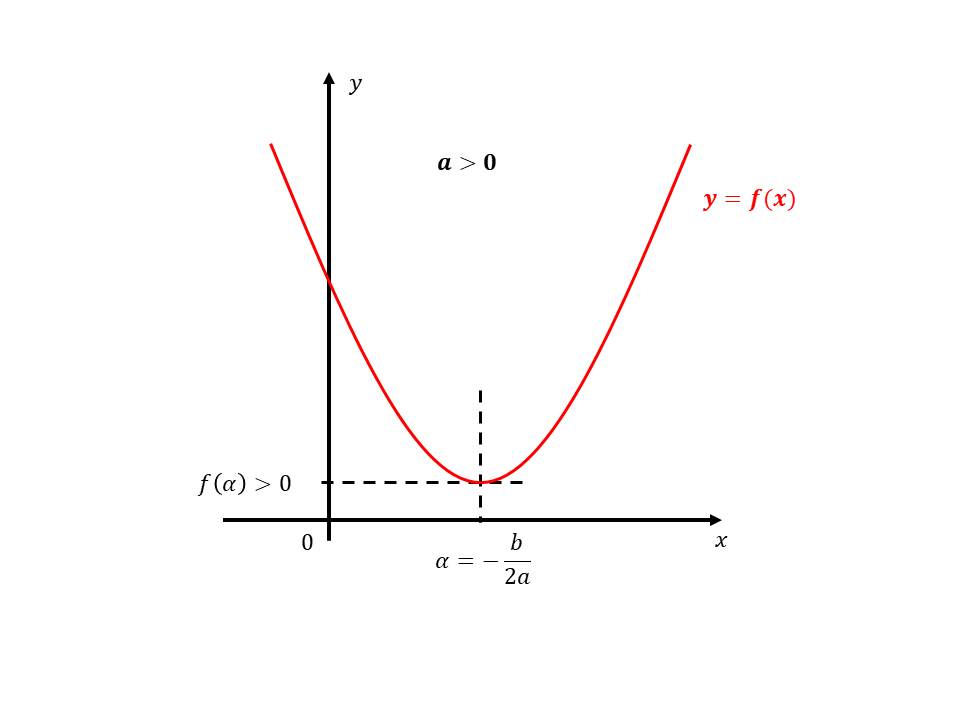
\(a<0\)

• \(\Delta < 0\)





• \(\Delta = 0\)





• \(\Delta > 0\)